Logistic regression

Lecture 10

Dr. Mine Çetinkaya-Rundel

Duke University
STA 101 - Fall 2023

Warm up

Check-in

  • Daily check-ins for getting you thinking at the beginning of the class and reviewing recent/important concepts
  • Go to Canvas and open today’s “quiz” titled 2023-10-09 Check-in
  • Access code: slopes (released in class)
  • “Graded” for completion

Project

  • Project workday on Friday in lab – use this time for finalizing and polishing, not getting started

  • Projects due Friday at 5 pm

  • Peer evaluations due Friday at 6 pm:

    • You’ll receive an email about them later today from TEAMMATES

    • You must turn in a peer evaluation to get the points your teammates awarded you

  • Only one person should submit the project on Gradescope and select all team members’ names. See https://sta101-f23.github.io/project/project-1.html#submission for more information.

Any questions about projects?

Logistic regression

So far in regression

  • Outcome: Numerical, Predictor: One numerical or one categorical with only two levels \(\rightarrow\) Simple linear regression

  • Outcome: Numerical, Predictors: Any number of numerical or categorical variables with any number of levels \(\rightarrow\) Multiple linear regression

  • Outcome: Categorical with only two levels, Predictors: Any number of numerical or categorical variables with any number of levels \(\rightarrow\) Logistic regression

  • Outcome: Categorical with any number of levels, Predictors: Any number of numerical or categorical variables with any number of levels \(\rightarrow\) Generalized linear models – Not covered in STA 101

Data + packages

library(tidyverse)
library(tidymodels)

hp_spam <- read_csv("data/hp-spam.csv")

  • 4601 emails collected at Hewlett-Packard labs and contains 58 variables

  • Outcome: type

    • type = 1 is spam

    • type = 0 is non-spam

  • Predictors of interest:

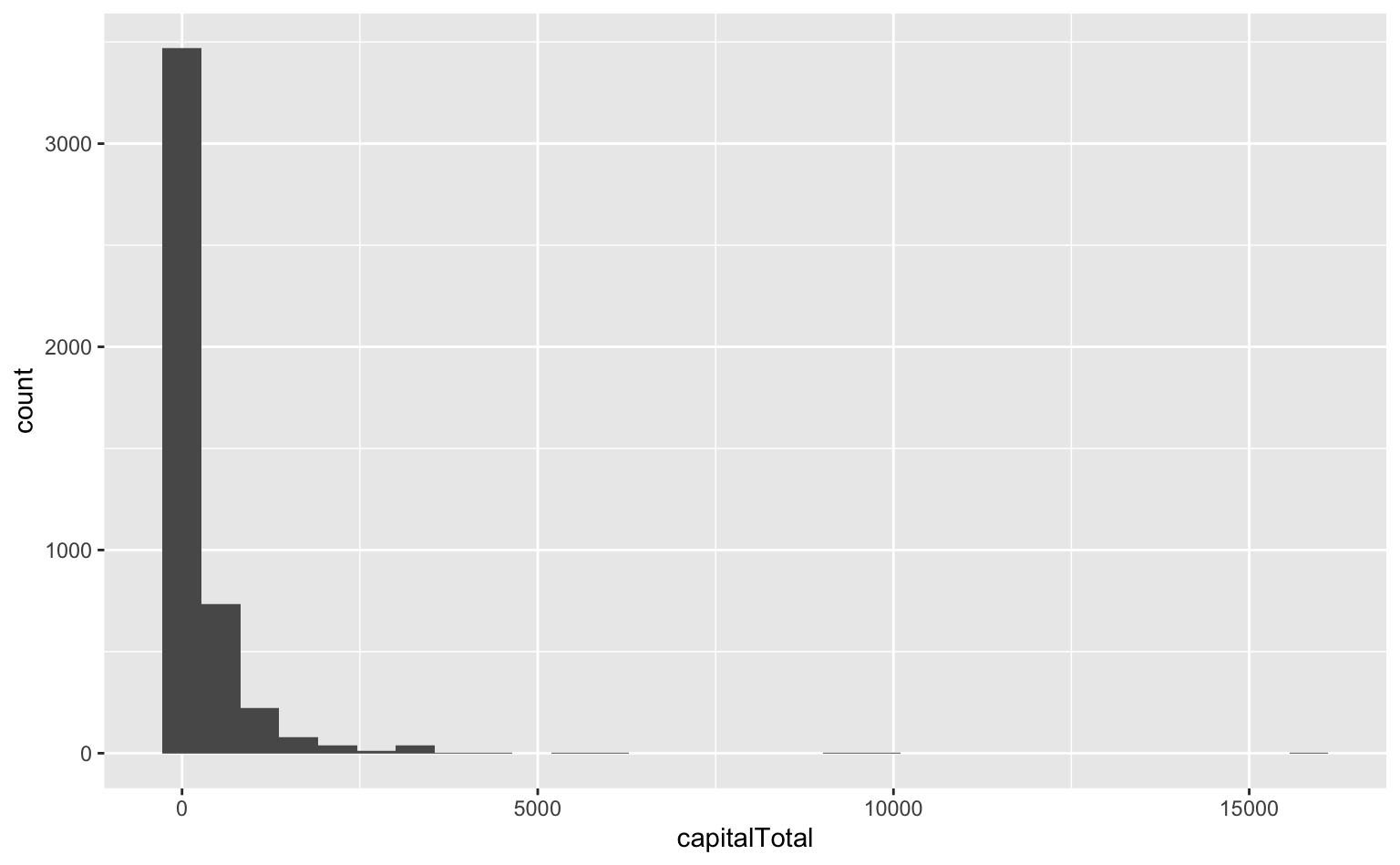
    • capitalTotal: Number of capital letters in email

    • Percentages are calculated as (100 * number of times the WORD appears in the e-mail) / total number of words in email

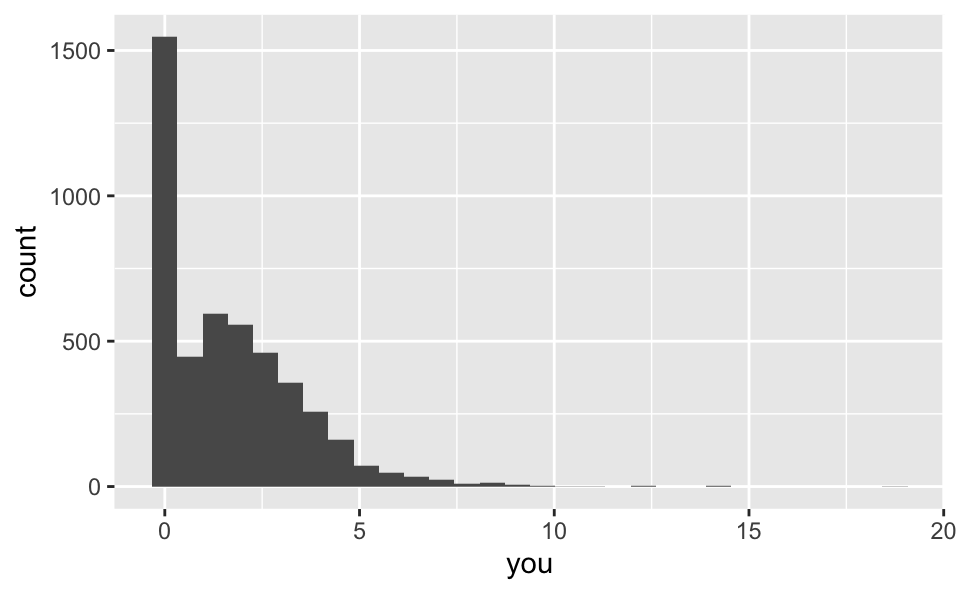
      • george: Percentage of “george”s in email (these were George’s emails)

      • you: Percentage of “you”s in email

Glimpse at data

What type of data is type? What type should it be in order to use logistic regression?

hp_spam |>
  select(type, george, capitalTotal, you)
# A tibble: 4,601 × 4
    type george capitalTotal   you
   <dbl>  <dbl>        <dbl> <dbl>
 1     1      0          278  1.93
 2     1      0         1028  3.47
 3     1      0         2259  1.36
 4     1      0          191  3.18
 5     1      0          191  3.18
 6     1      0           54  0   
 7     1      0          112  3.85
 8     1      0           49  0   
 9     1      0         1257  1.23
10     1      0          749  1.67
# ℹ 4,591 more rows

EDA: How much spam?

hp_spam |>
  count(type) |>
  mutate(p = n / sum(n))
# A tibble: 2 × 3
   type     n     p
  <dbl> <int> <dbl>
1     0  2788 0.606
2     1  1813 0.394

EDA: AM I SCREAMING? capitalTotal

ggplot(hp_spam, aes(x = capitalTotal)) +
  geom_histogram()

EDA: george, is that you?

ggplot(hp_spam, aes(x = george)) +
  geom_histogram()
ggplot(hp_spam, aes(x = you)) +
  geom_histogram()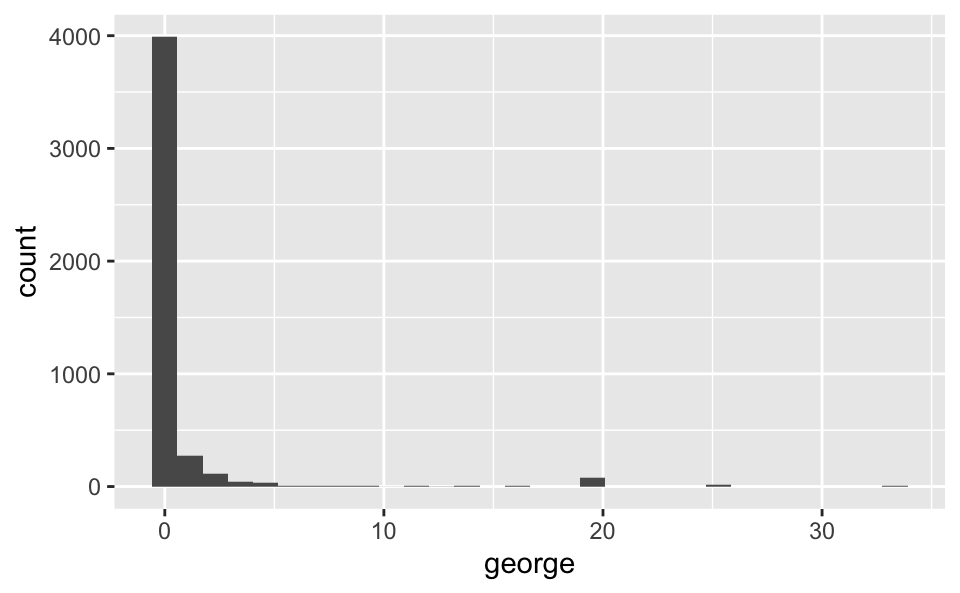

Logistic regression

  • Logistic regression takes in a number of predictors and outputs the probability of a “success” (an outcome of 1) in a binary outcome variable.

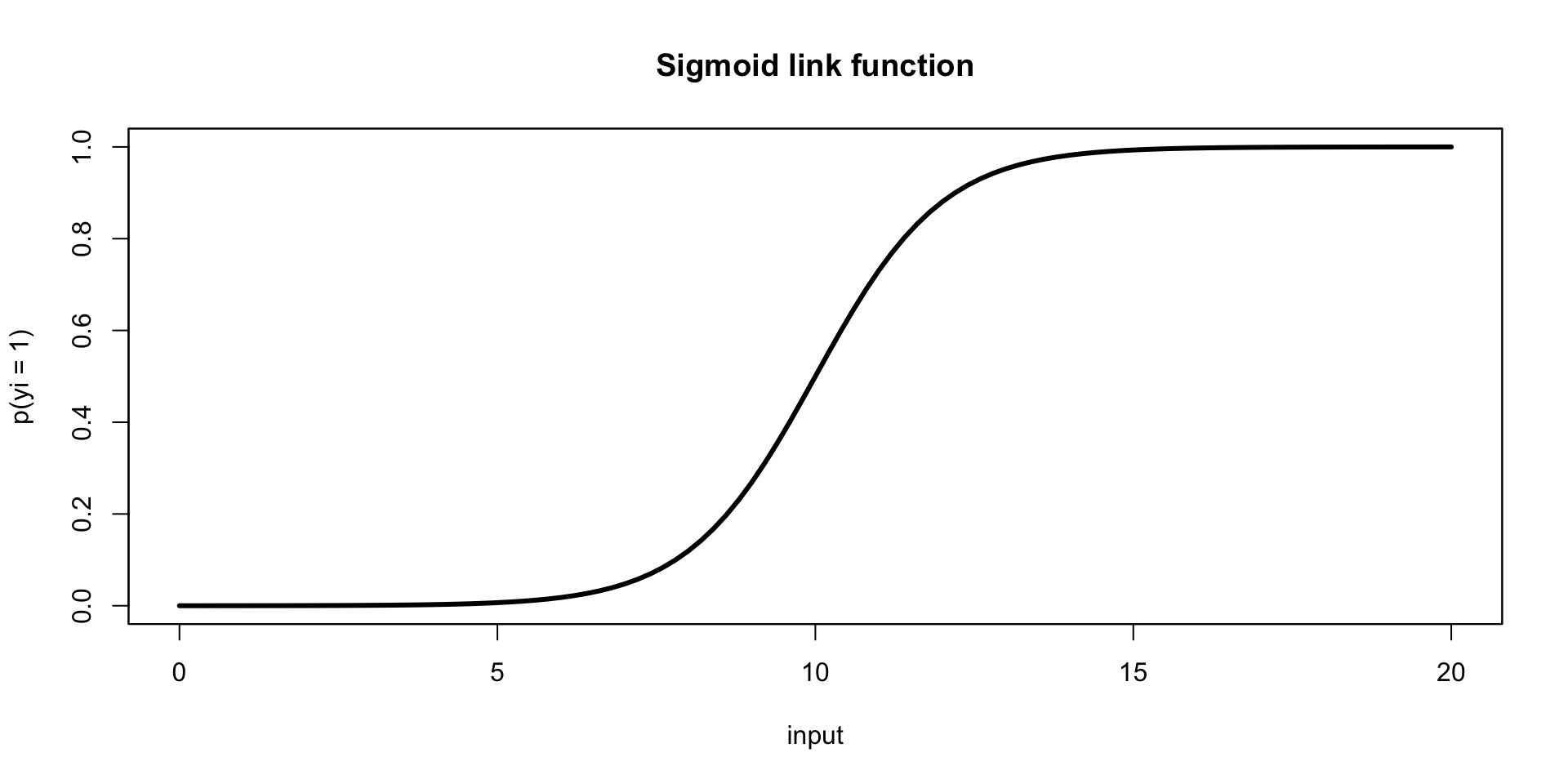
  • The probability is related to the predictors via a sigmoid link function, \[ p(y_i = 1) = \frac{1}{1+\text{exp}({- \sum \beta_i x_i })}, \]whose output is in \((0,1)\) (a probability).

  • In this modeling scheme, one typically finds \(\hat{\beta}\) by maximizing the likelihood function, another objective function, different than our previous “least squares” objective.

Logistic regression, visualized

Using data to estimate \(\beta_i\)

To proceed with building our email classifier, we will, as usual, use our data (outcome \(y_i\) and predictor \(x_i\) pairs), to estimate \(\beta\) (find \(\hat{\beta}\)) and obtain the model: \[ p(y_i = 1) = \frac{1}{1+\text{exp}({- \sum \hat{\beta}_i x_i})}, \]

Application exercise

Go to Posit Cloud and continue the project titled ae-09-Spam.

ICYMI

Today’s daily check-in access code: slopes (released in class)

🔗 sta101-f23.github.io