Overview: Inference for proportions

Lecture 19

Dr. Mine Çetinkaya-Rundel

Duke University
STA 101 - Fall 2023

Warm up

Exam 2

  • Classroom: You should have received your exam location assignment last night. Reach out to me ASAP if you haven’t received it.
  • In-class: On Wednesday
    • 1 page, both sides notes (“cheat sheet”)
    • Nothing else
  • Take-home: Wednesday - Friday
    • Open everything except for other humans, except for me :)

Office hours this week

From last time

Inference for two-way proportions

First:

Vote on Canvas under 2023-11-13 Check-in with the access code twoway.

Then:

Go to Posit Cloud and continue the project titled ae-14 - Candidate talk.

Overview

Married at 25

A study suggests that the 25% of 25 year olds have gotten married. You believe that this is incorrect and decide to collect your own sample for a hypothesis test. From a random sample of 25 year olds in census data with size 776, you find that 24% of them are married.

What is 776? What is 24%?

Married at 25

A study suggests that the 25% of 25 year olds have gotten married. You believe that this is incorrect and decide to collect your own sample for a hypothesis test. From a random sample of 25 year olds in census data with size 776, you find that 24% of them are married. A friend of yours offers to help you with setting up the hypothesis test and comes up with the following hypotheses. Indicate any errors you see.

\[ \begin{aligned} H_0: \hat{p} = 0.24 \\ H_A: \hat{p} \ne 0.24 \end{aligned} \]

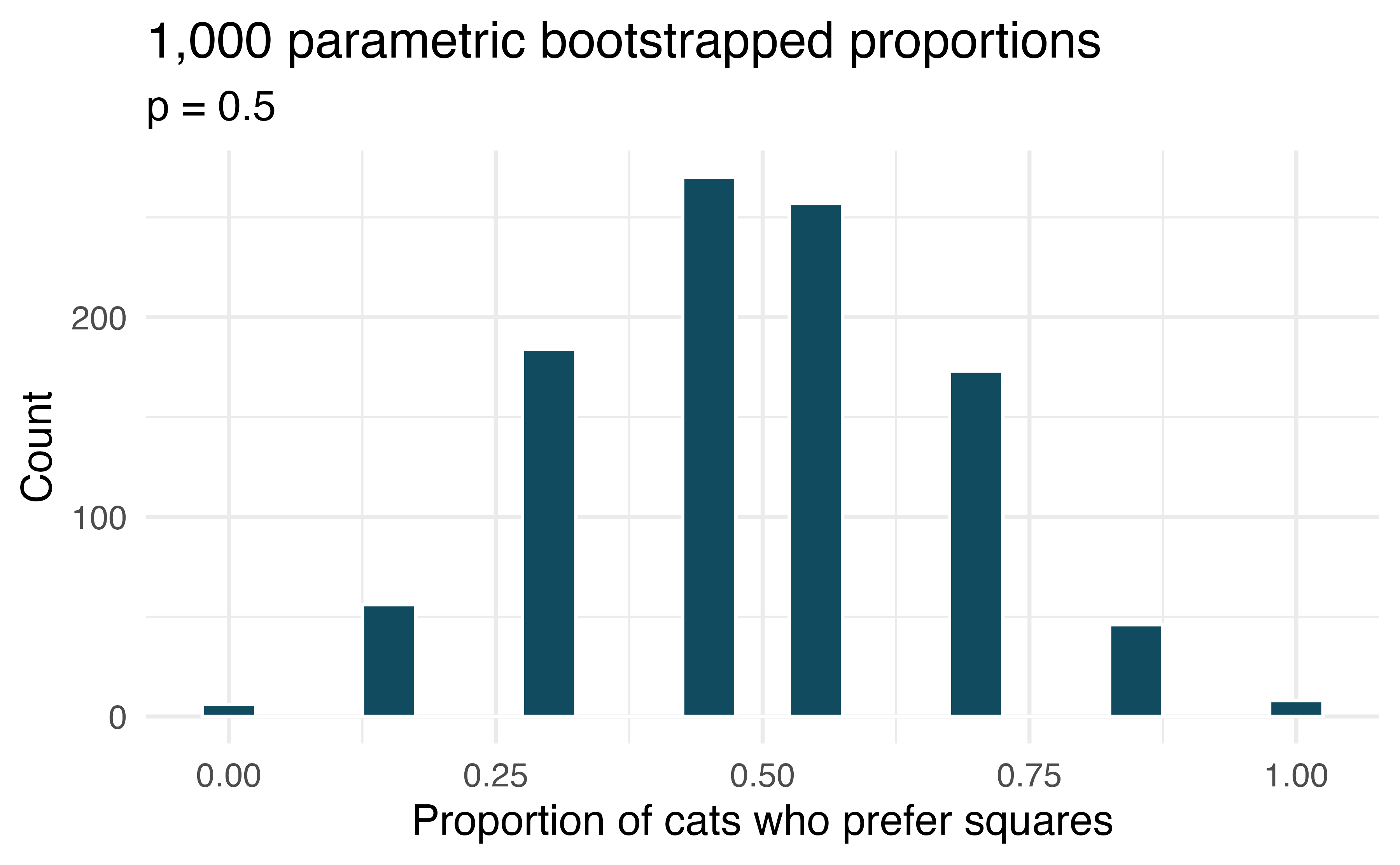
If I fits, I sits

A citizen science project on which type of enclosed spaces cats are most likely to sit in compared (among other options) two different spaces taped to the ground. The first was a square, and the second was a shape known as Kanizsa square illusion. When comparing the two options given to 7 cats, 5 chose the square, and 2 chose the Kanizsa square illusion. We are interested to know whether these data provide convincing evidence that cats prefer one of the shapes over the other.

What are the null and alternative hypotheses for evaluating whether these data provide convincing evidence that cats have preference for one of the shapes.

If I fits, I sits

A parametric bootstrap simulation (with 1,000 bootstrap samples) was run and the resulting null distribution is displayed in the histogram below. Find the p-value using this distribution and conclude the hypothesis test in the context of the problem.

Legalization of marijuana

The 2018 General Social Survey asked a random sample of 1,563 US adults: “Do you think the use of marijuana should be made legal, or not?” 60% of the respondents said it should be made legal. Consider a scenario where, in order to become legal, 55% (or more) of voters must approve.

What are the null and alternative hypotheses for evaluating whether these data provide convincing evidence that, if voted on, marijuana would be legalized in the US.

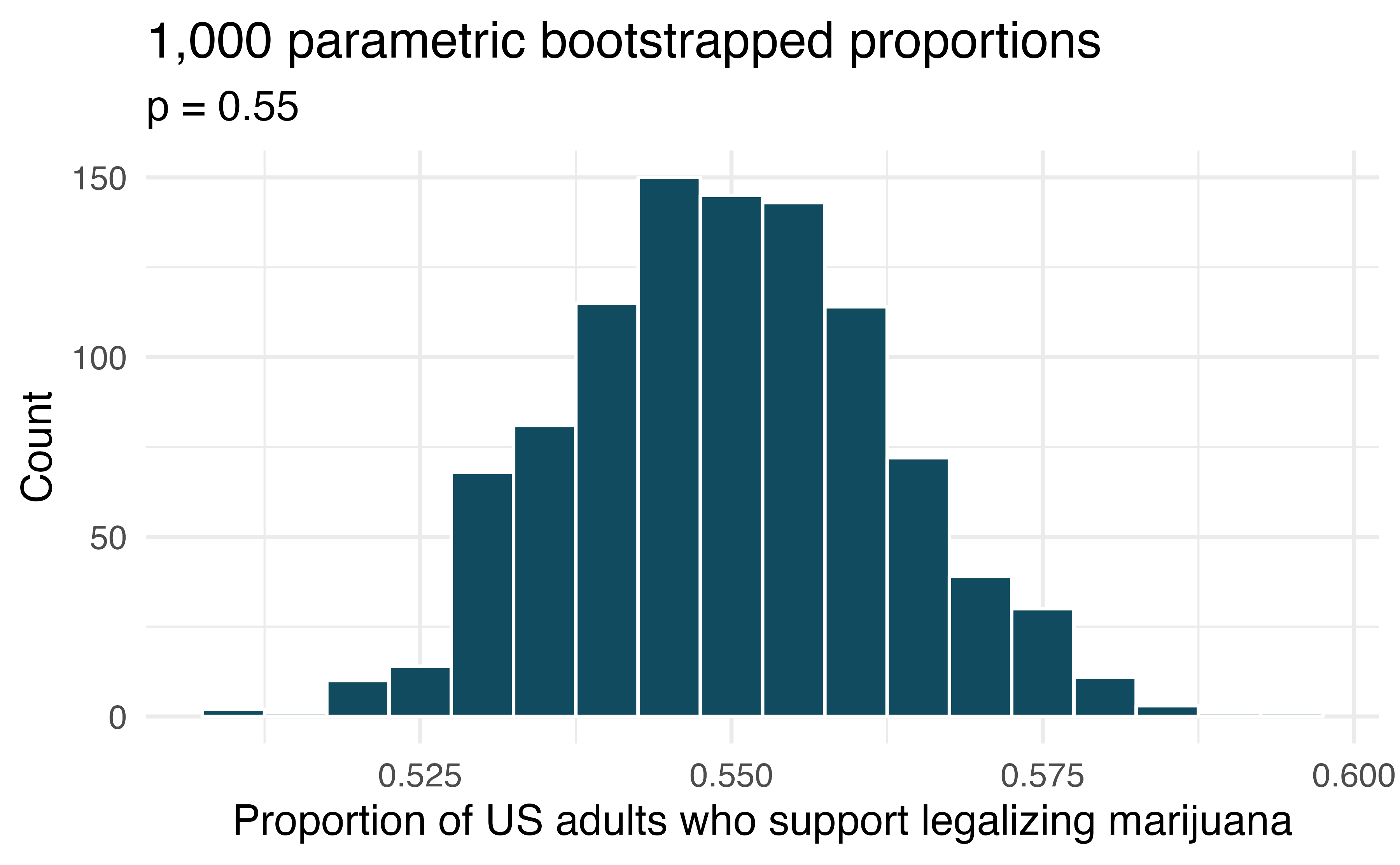
Legalization of marijuana

A parametric bootstrap simulation (with 1,000 bootstrap samples) was run and the resulting null distribution is displayed in the histogram below. Find the p-value using this distribution and conclude the hypothesis test in the context of the problem.

Legalization of marijuana - SE calculate

According to the 2018 General Social Survey, in a random sample of 1,563 US adults, 60% think marijuana should be made legal. Consider a scenario where, in order to become legal, 55% (or more) of voters must approve.

Calculate the standard error of the sample proportion using the mathematical model.

Note

The standard error of the sample proportion is \(\sqrt{\frac{p(1-p)}{n}}\), however since we don’t know \(p\) and, in the context of a confidence interval, don’t have a null hypothesis governing what we should assume for the value of \(p\), we estimate it with the sample proportion, yielding:

\[ SE_{\hat{p}} = \sqrt{ \frac{\hat{p}(1 - \hat{p})}{n} } \]

Legalization of marijuana - SE estimate

A parametric bootstrap simulation (with 1,000 bootstrap samples) was run and the resulting null distribution is displayed in the histogram below. This distribution shows the variability of the sample proportion in samples of size 1,563 when 55% of voters approve legalizing marijuana. What is the approximate standard error of the sample proportion based on this distribution?

Legalization of marijuana - compare SEs

Do the mathematical model and parametric bootstrap give similar standard errors?

Legalization of marijuana - compare methods

In this setting (to test whether the true underlying population proportion is greater than 0.55), would there be a strong reason to choose the mathematical model over the parametric bootstrap (or vice versa)?

Note

Technical conditions for constructing a confindence interval for a proportion:

  1. Independence: The observations in the sample must be independent of each other with respect to the response variable.
  2. Large enough sample: Number of observed successes and failures must be at least 10.

Legalization of marijuana - compare methods

The General Social Survey asked a random sample of 1,563 US adults: “Do you think the use of marijuana should be made legal, or not?” 60% of the respondents said it should be made legal.

Legalization of marijuana - mathematical interval

The General Social Survey asked a random sample of 1,563 US adults: “Do you think the use of marijuana should be made legal, or not?” 60% of the respondents said it should be made legal.

  1. Is 60% a sample statistic or a population parameter? Explain.

  2. Using a mathematical model, construct a 95% confidence interval for the proportion of US adults who think marijuana should be made legal, and interpret it.

  3. A critic points out that this 95% confidence interval is only accurate if the statistic follows a normal distribution, or if the normal model is a good approximation. Is this true for these data? Explain.

  4. A news piece on this survey’s findings states, “Majority of US adults think marijuana should be legalized.” Based on your confidence interval, is this statement justified?

🔗 sta101-f23.github.io