Issues candidates should talk more about

Application exercise
Suggested answers

In this application exercise, we’ll do inference tables – categorical variables with many levels.

Packages

We’ll use the tidyverse and tidymodels packages.

library(tidyverse)
library(tidymodels)
library(ggthemes)

Data

A September 16-19, 2023, asked North Carolina voters, among other issues, about issues of equality and women’s progress. Specifically, one of the questions asked:

If you had to choose just one issue that you would like candidates to talk more about in the 2024 campaigns, what would that issue be?

  • Economy

  • Abortion/Reproductive rights

  • Immigration

  • Crime

  • Gun rights/restrictions

  • Something else

  • Don’t know

The survey also asked respondents’ party affiliation:

What political party do you most identify with?

  • Democrat

  • Republican

  • Unaffiliated

  • Other

The results of this survey are summarized in this report and the data can be found in your data folder: candidate-talk.csv.

Hypotheses

Exercise 1

State the hypotheses for evaluating whether the issue of choice is independent of party affiliation.

H0: Issue of choice and party affiliation are independent.

HA: Issue of choice and party affiliation are independent.

Data

Exercise 2

Load the data.

candidate_talk <- read_csv("data/candidate-talk.csv")

Exercise 3

Create a two-way table of the responses across the two age groups and visualize the frequency distribution.

candidate_talk <- candidate_talk |>
  mutate(
    party = fct_relevel(party, "Democrat", "Republican", "Unaffiliated", "Other"),
    issue = fct_relevel(issue, "Abortion/Reproductive rights", "Crime", "Economy", "Gun rights/restrictions", "Immigration", "Something else", "Don't know")
  )

candidate_talk_table <- candidate_talk |>
  count(party, issue) |>
  pivot_wider(names_from = "issue", values_from = "n")

candidate_talk_table
# A tibble: 4 × 8
  party  Abortion/Reproductiv…¹ Crime Economy Gun rights/restricti…² Immigration
  <fct>                   <int> <int>   <int>                  <int>       <int>
1 Democ…                     70    22      94                     59          10
2 Repub…                     21    35     138                     14          76
3 Unaff…                     20    10      79                     16          20
4 Other                       4     4      14                      4           5
# ℹ abbreviated names: ¹​`Abortion/Reproductive rights`,
#   ²​`Gun rights/restrictions`
# ℹ 2 more variables: `Something else` <int>, `Don't know` <int>
ggplot(candidate_talk, aes(x = party, fill = issue)) +
  geom_bar() +
  scale_fill_colorblind()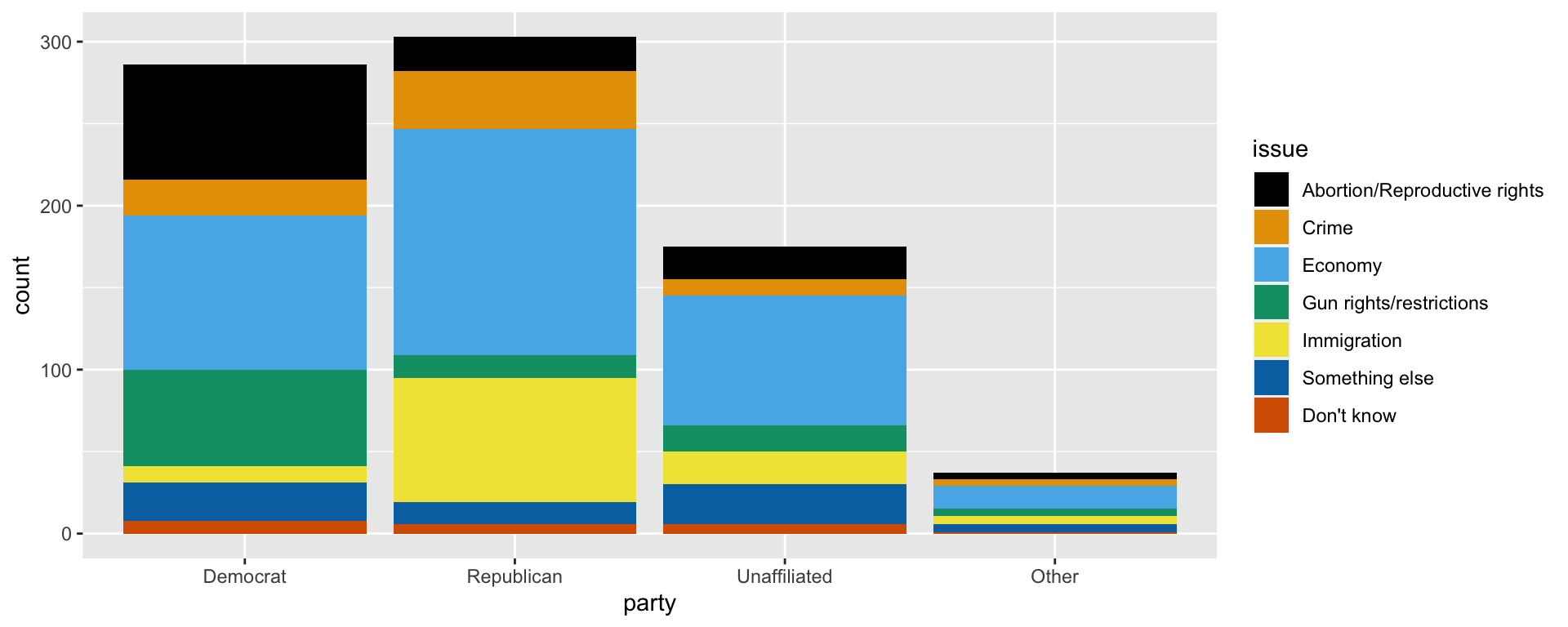

Exercise 4

Which do you think should be the explanatory variable and which the response variable? Accordingly, create a visualization that shows the correct conditional probabilities.

ggplot(candidate_talk, aes(x = party, fill = issue)) +
  geom_bar(position = "fill") +
  scale_fill_colorblind()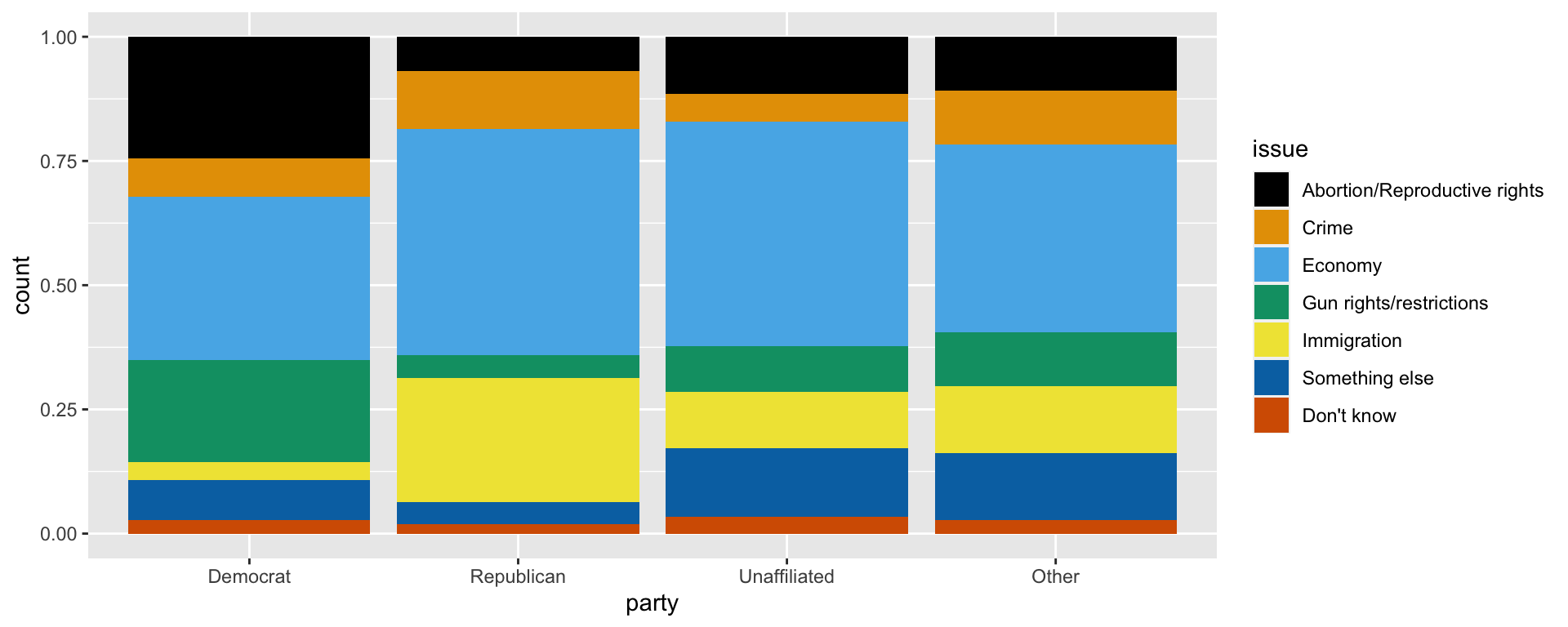

Testing

Exercise 5

Calculate the observed sample statistic.

obs_stat <- candidate_talk |>
  specify(response = issue, explanatory = party) |>
  hypothesize(null = "independence") |>
  calculate(stat = "Chisq")

obs_stat
Response: issue (factor)
Explanatory: party (factor)
Null Hypothesis: independence
# A tibble: 1 × 1
   stat
  <dbl>
1  144.

Exercise 6

Conduct the hypothesis test using randomization and visualize and report the p-value.

set.seed(1234)

null_dist <- candidate_talk |>
  specify(response = issue, explanatory = party) |>
  hypothesize(null = "independence") |>
  generate(reps = 1000, type = "permute") |>
  calculate(stat = "Chisq")

null_dist |>
  get_p_value(obs_stat = obs_stat, direction = "greater")
Warning: Please be cautious in reporting a p-value of 0. This result is an
approximation based on the number of `reps` chosen in the `generate()` step.
See `?get_p_value()` for more information.
# A tibble: 1 × 1
  p_value
    <dbl>
1       0
null_dist |>
  visualize() +
  shade_p_value(obs_stat = obs_stat, direction = "greater")
Warning in min(diff(unique_loc)): no non-missing arguments to min; returning
Inf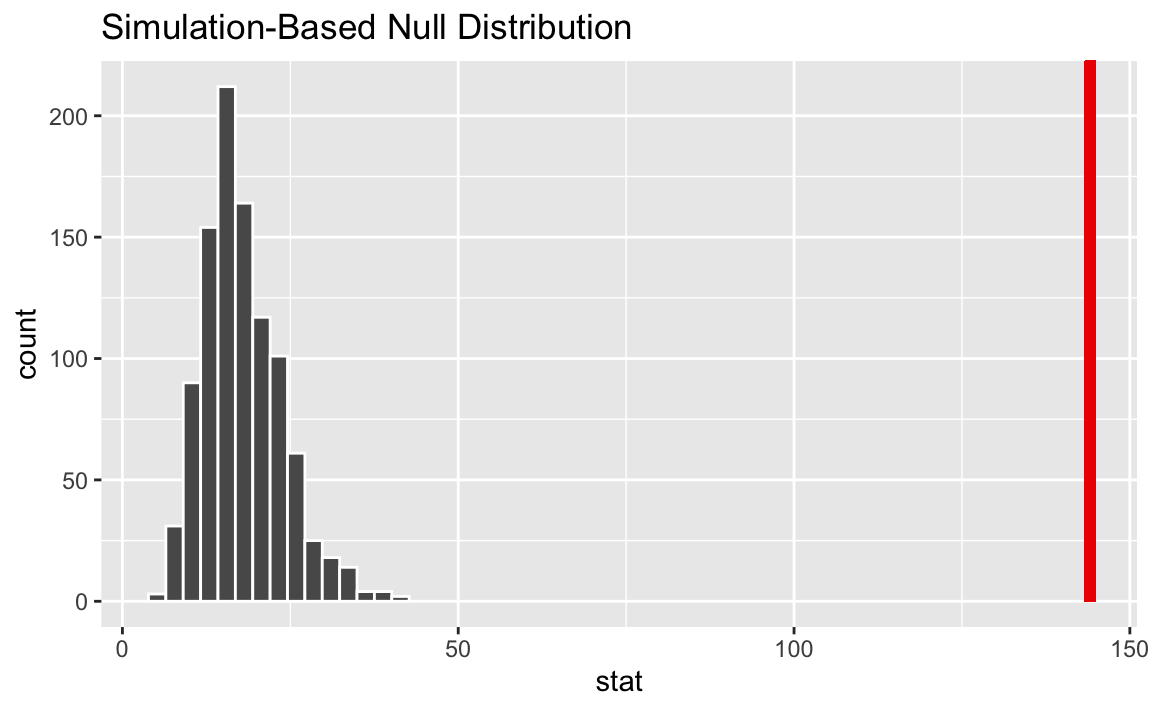

Exercise 7

What is the conclusion of the hypothesis test?

With a p-value of approximately 0, which is smaller than the discernability level of 0.05, we reject the null hypothesis. The data provide convincing evidence that there is a relationship between party affiliation and issues voters want candidates to discuss.