Climate change

Application exercise

In this application exercise, we’ll do inference for a comparing two paired means and many means.

Packages

We’ll use the tidyverse, tidymodels, openintro, and ggthemes packages.

library(tidyverse)
library(tidymodels)
library(openintro)

Paired means

Throughout this application exercise, we’ll make use of the climate70 dataset supplied by the openintro package.

glimpse(climate70)

Rows: 197
Columns: 7
$ station   <fct> USC00203823, USC00276818, USC00186620, USC00331890, USC00235…
$ latitude  <dbl> 41.93520, 44.25800, 39.41317, 40.24030, 37.83950, 45.56550, …
$ longitude <dbl> -84.64110, -71.25250, -79.40025, -81.87100, -94.37400, -100.…
$ dx70_1948 <int> 131, 80, 143, 156, 216, 138, 131, 194, 198, 213, 224, 74, 17…
$ dx70_2018 <int> 147, 99, 150, 158, 175, 132, 129, 188, 240, 213, 191, 101, 2…
$ dx90_1948 <int> 11, 1, 4, 18, 59, 39, 23, 17, 46, 67, 49, 0, 34, 35, 71, 100…
$ dx90_2018 <int> 16, 1, 1, 15, 51, 18, 17, 3, 65, 104, 39, 0, 62, 3, 86, 117,…

The question we want to answer is: Do these data provide convincing evidence that the number of days above 90 degrees between 2018 and 1948?

First, let’s set the hypotheses.

Add response here.

To carry out inference on paired data, we pre-compute the difference between paired values at the beginning of the analysis, and use those differences as our values of interest.

climate70 <- climate70 |>
  mutate(dx90_diff = dx90_2018 - dx90_1948)

climate70 |>
   select(station, latitude, longitude, contains("dx90"))

# A tibble: 197 × 6
   station     latitude longitude dx90_1948 dx90_2018 dx90_diff
   <fct>          <dbl>     <dbl>     <int>     <int>     <int>
 1 USC00203823     41.9     -84.6        11        16         5
 2 USC00276818     44.3     -71.3         1         1         0
 3 USC00186620     39.4     -79.4         4         1        -3
 4 USC00331890     40.2     -81.9        18        15        -3
 5 USC00235987     37.8     -94.4        59        51        -8
 6 USC00395691     45.6    -100.         39        18       -21
 7 USC00219046     43.8     -94.2        23        17        -6
 8 USW00003812     35.4     -82.5        17         3       -14
 9 USC00047643     38.5    -122.         46        65        19
10 USW00013896     34.7     -87.6        67       104        37
# ℹ 187 more rows

And then visualize these differences:

ggplot(climate70, aes(x = dx90_diff)) +
  geom_histogram()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.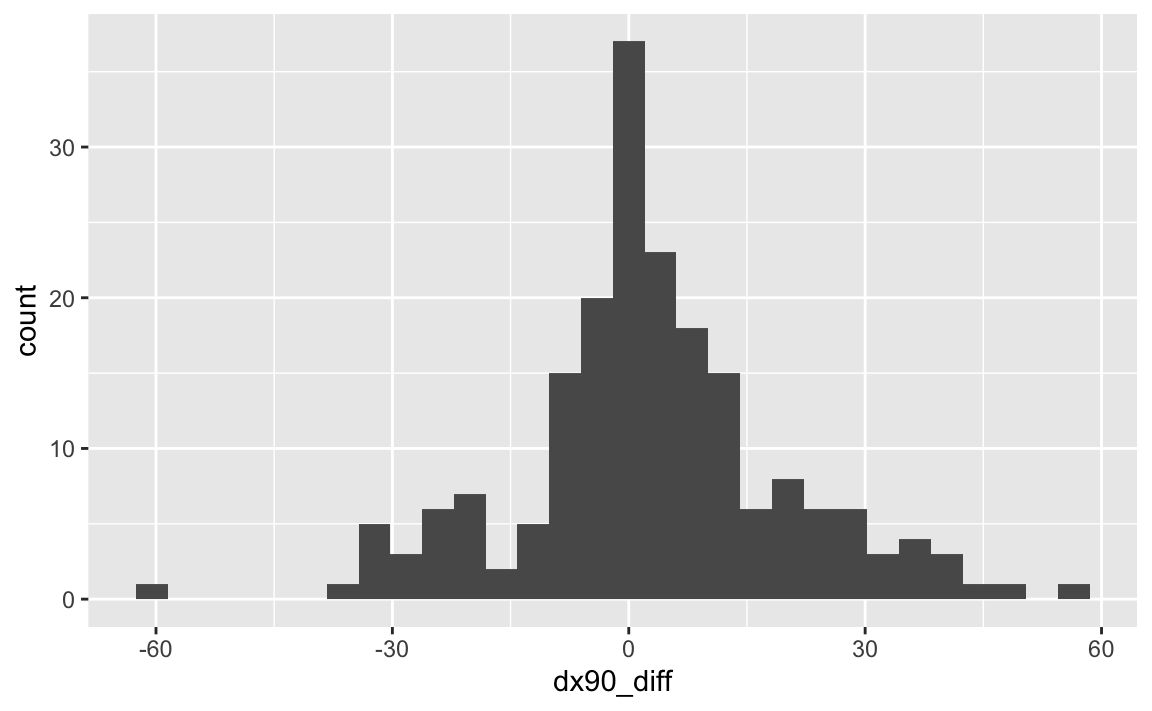

We calculate the observed statistic in the paired setting in the same way that we would outside of the paired setting. Using specify() and calculate():

obs_stat <- climate70 |> 
  specify(response = dx90_diff) |> 
  calculate(stat = "mean")

obs_stat

Response: dx90_diff (numeric)
# A tibble: 1 × 1
   stat
  <dbl>
1  2.90

Now, we want to compare this statistic to a null distribution, generated under the assumption that the true difference was actually zero, to get a sense of how likely it would be for us to see this observed difference or something more extreme.

Tests for paired data are carried out via the null = "paired independence" argument to hypothesize().

set.seed(1129)

null_dist <- climate70 |> 
   specify(response = dx90_diff) |> 
   hypothesize(null = "paired independence") |>
   generate(reps = 1000, type = "permute") |>
   calculate(stat = "mean")
   
visualize(null_dist)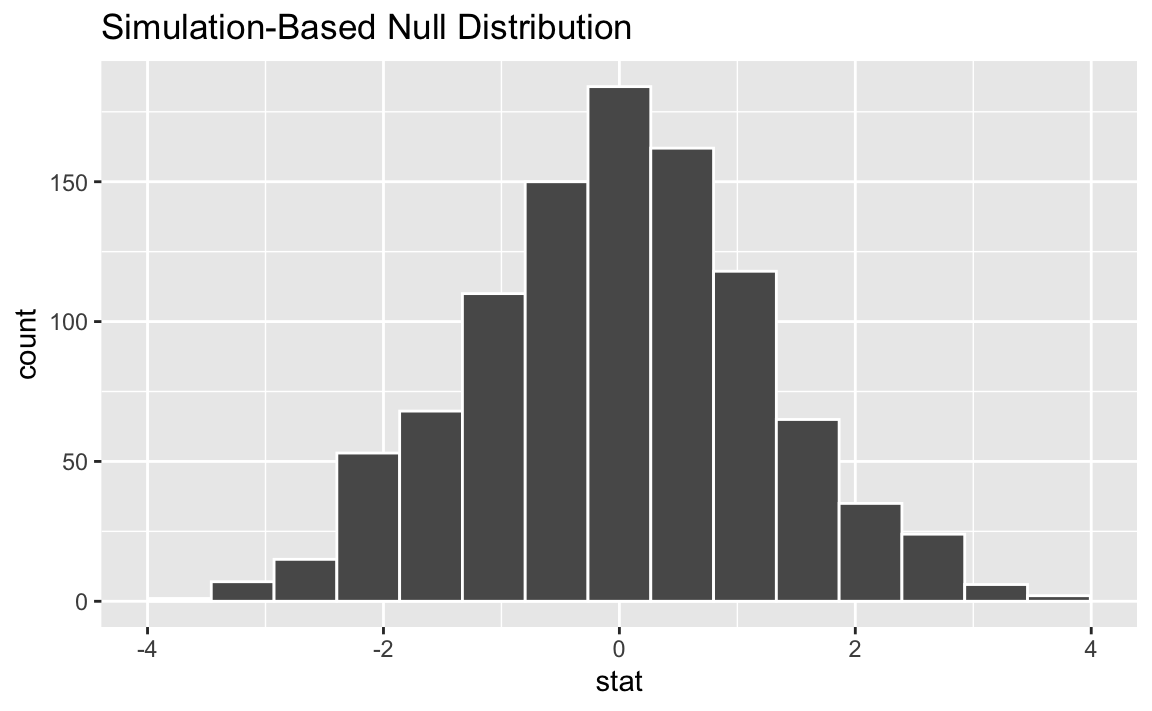

For each replicate, generate() carries out type = "permute" with null = "paired independence" by:

Randomly sampling a vector of signs (i.e., -1 or 1), probability 0.5 for either, with length equal to the input data, and
Multiplying the response variable by the vector of signs, “flipping” the observed values for a random subset of value in each replicate

To get a sense for what this distribution looks like, and where our observed statistic falls, we can use visualize():

visualize(null_dist) + 
  shade_p_value(obs_stat, direction = "two-sided")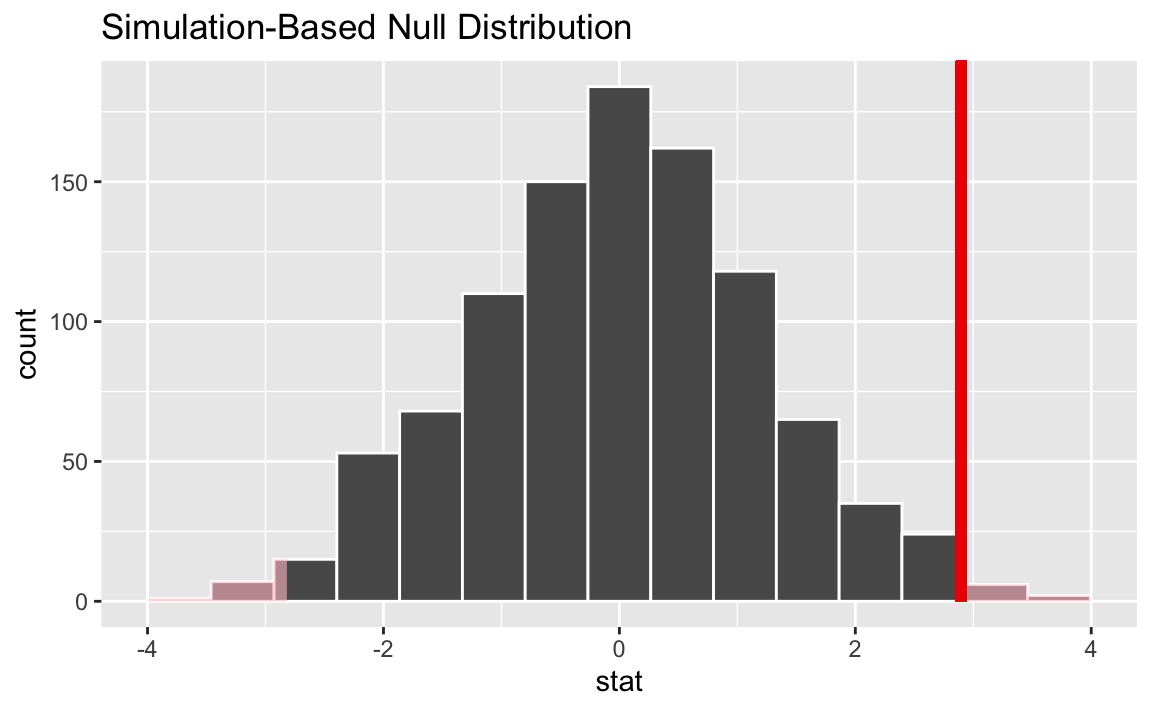

Then, we calculate the p-value:

p_value <- null_dist |>
  get_p_value(obs_stat, direction = "two-sided")

p_value

# A tibble: 1 × 1
  p_value
    <dbl>
1   0.016